Big O Notation & Time Complexity Basics (Understanding Algorithm Efficiency)

Why Big O Notation Matters in the Real World

Have you ever built a program that worked fine at first, only to slow down as the data grew? Maybe your app was snappy with a few users but became sluggish under heavy load. This happens when algorithms aren’t designed to scale efficiently.

Big O notation helps you anticipate performance bottlenecks before they slow down your application, letting you choose smarter algorithms upfront. Whether you're handling large datasets, optimising search functions, or improving API response times, the right algorithm can mean the difference between a smooth experience and a frustrating slowdown.

Let’s break it down with real-world examples so you can recognise inefficient patterns and write smarter, scalable code

Breaking Down Big O Notation

Big O notation might seem like an abstract concept, but it has real-world consequences. Have you ever wondered why some programs handle millions of users effortlessly while others crash under pressure? It all comes down to how they scale.

As applications grow, performance can be the difference between a seamless experience and a slow, unusable system. Understanding Big O helps you predict how your code will behave as the input sise increases.

Instead of just talking about complexity, let’s visualise how different time complexities scale and what that means for performance.

The best way to understand Big O is to see it in action. Let’s break down how different time complexities behave and what they mean for your code.

Some algorithms handle growth smoothly, while others slow to a crawl as input increases. The graph below gives a visual sense of how different complexities scale—helping you spot performance pitfalls before they happen.

Key takeaway:

• Flat lines (O(1)) mean the algorithm doesn't slow down as the input grows.
• Steep curves (O(n²), O(2ⁿ)) signal rapid slowdowns as input sise increases.
• Logarithmic growth (O(log n)) shows a pattern of efficiency where each step reduces the remaining work.

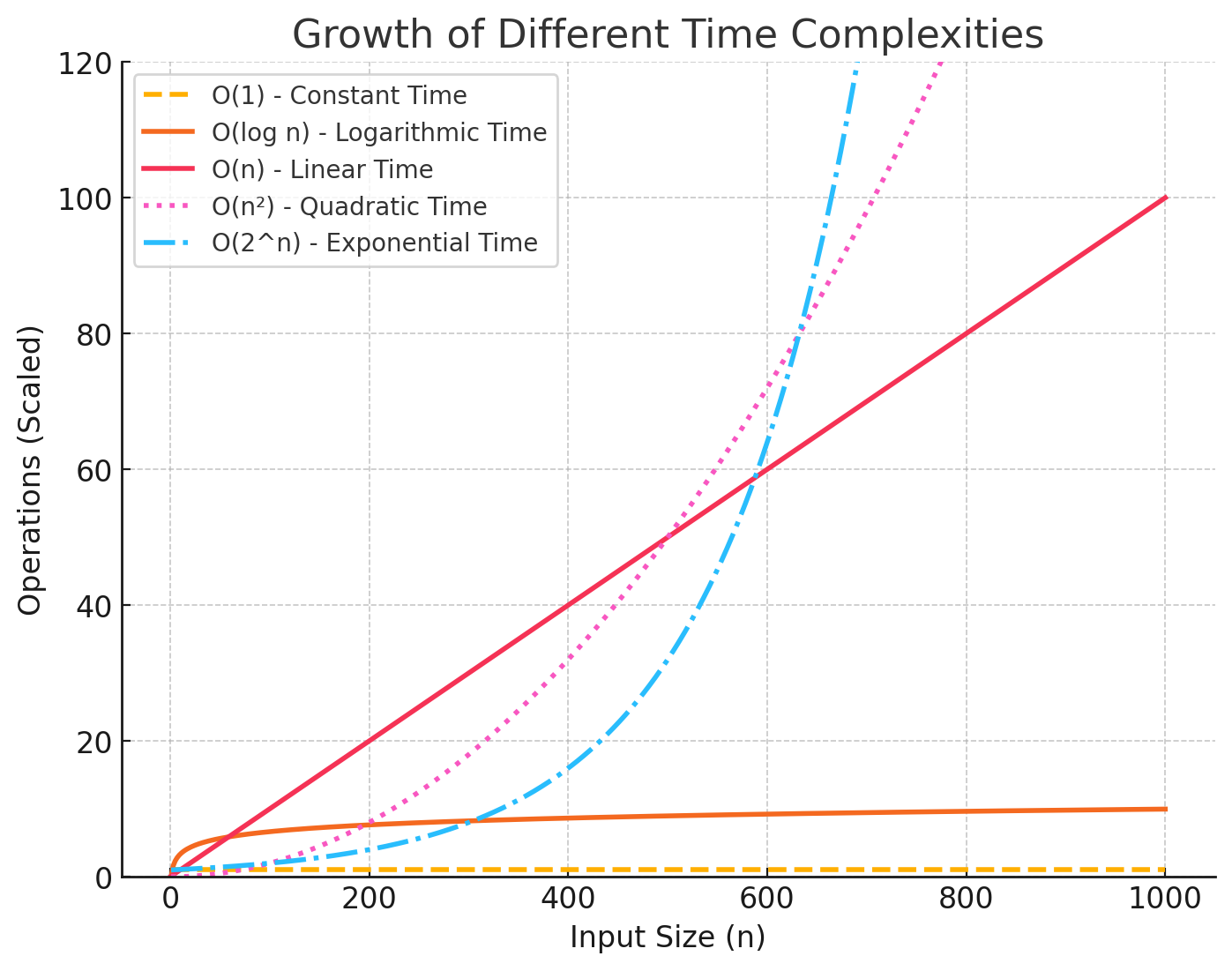
This graph illustrates how constant, logarithmic, linear, quadratic, and exponential complexities scale with input sise.

O(1) – Constant Time

Accessing a single piece of data in an array takes the same amount of time, whether the array has ten elements or ten million. That’s O(1)—the operation remains constant regardless of input sise.

Example: Accessing an element in an array by index (arr[5]).

arr = [10, 20, 30, 40, 50]
print(arr[3])  # Always takes the same time

Real-World Scenario: Checking if a user is logged in using a boolean flag.

O(log n) – Logarithmic Time

When searching for a word in a large dictionary, you wouldn’t flip through every page sequentially. Instead, you jump to the middle, decide whether to go left or right, and keep halving the search space. That’s O(log n)—each step significantly reduces the number of possibilities.

Example: Searching in a sorted array.

# Searching for a number in a sorted list? Instead of scanning through one by one, let's be smarter. Think about guessing a number between 1 and 100—you don’t start at 1 and count up. You jump to the middle and keep halving. That’s binary search!
def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

Real-World Scenario: Indexing a product catalog for fast search instead of scanning the entire dataset every time.

O(n) – Linear Time

Processing a log file where you need to scan each line to find a specific error message takes time proportional to the number of lines. The more lines, the longer it takes—this is O(n), where execution time grows linearly with input sise.

Example: Finding the maximum value in a list.

def find_max(arr):
    max_val = arr[0]
    for num in arr:
        if num > max_val:
            max_val = num
    return max_val

Real-World Scenario: Searching for a user ID in an unsorted list, which requires scanning through each entry one by one.

O(n²) – Quadratic Time

Ever tried tagging friends in a group photo manually? If you go one by one, checking each friend against all the others, it quickly becomes overwhelming. That’s O(n²)—and why social networks use smarter algorithms to avoid this mess. As the number of users grows, the comparisons increase significantly—this is O(n²).

Example: Checking for duplicate values in a list using nested loops.

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

Real-World Scenario: Checking for duplicate records in a dataset using nested loops instead of a hash set.

O(2ⁿ) – Exponential Time

Some problems spiral out of control faster than you might expect. That’s O(2ⁿ) for you. Each function call spawns two more, then those spawn two more, and soon enough, you’ve got an explosion of calculations that your CPU won’t be happy about!

Example: Recursive Fibonacci sequence and its optimised version with memoisation.

def fibonacci(n):
    if n <= 1:
        return n
    return fibonacci(n-1) + fibonacci(n-2)

Real-World Scenario: Brute-force password cracking, where each additional character exponentially increases the number of possibilities, or generating all possible subsets of a set (power set generation).

Thinking Like a Performance-Driven Developer

Now that we’ve broken down Big O notation, how do you actually apply it in real-world coding? Let’s go beyond definitions and focus on strategies to write more efficient code.

Understanding Big O isn’t just about memorising definitions—it’s about spotting inefficiencies before they become problems. Let’s explore practical ways to apply Big O thinking to your coding decisions.

1. Identify the Bottleneck in Your Code

When analysing an algorithm, focus on what grows the fastest. The slowest part of your code will usually determine its performance limit.

If an algorithm has multiple steps, the term that grows the fastest dominates. For example:

# O(n² + n) simplifies to O(n²)
for i in range(n):
    for j in range(n):
        print(i, j)  # O(n²)

for k in range(n):
    print(k)  # O(n)

2. Cut Down Unnecessary Work

Efficient coding isn't just about writing fewer lines—it’s about reducing redundant calculations and optimising loops.

Example: Instead of recalculating values in loops, store them.

# Bad: O(n²)
for i in range(n):
    for j in range(n):
        sum_val = sum(arr)  # Unnecessary recalculations

# Good: O(n)
total_sum = sum(arr)
for i in range(n):
    print(total_sum)

3. Recognising Slow Code Before It Hurts Performance

Certain coding patterns lead to inefficiencies. By recognising them early, you can make smarter choices about data structures and algorithms.

• Sorting algorithms: Usually O(n log n) (like Merge Sort or Quick Sort).
• Graph traversal (BFS, DFS): Typically O(V + E), where V = vertices, E = edges.
• Hash table lookups: O(1) on average, O(n) in worst-case collisions.

Final Challenge: Put Your Knowledge to the Test!

Want to solidify your understanding of Big O notation? Try this:

Scenario: You need to find the two largest numbers in an unsorted list. What’s the most efficient way to do this, and what’s its time complexity?

Your turn! You need to find the two largest numbers in an unsorted list—fast. Do you sort first? Use a single pass? What's the smartest way? Code it, time it, and prove you found the best solution! Share your best solution! Let me know your approach!

At first, Big O notation might seem abstract, but once you apply it, you'll see how it improves your code. Understanding time complexity helps you write more scalable, efficient software, preventing performance bottlenecks before they happen. Give it a try—optimise your own code and see the difference!